□ Tren
Data yang memiliki pergerakkan sedikit demi sedikit meningkat atau menurun. karena mengalami pengaruh perubahan pendapatan, popuasi, penyebaran umur, atau pendangan budaya.
Model Tren Linear adalah suatu tren yang diramalkan naik atau turun secara garis lurus. Ada dua jenis :
- Medode Least Square
- Metode Moment
Model Tren Non Linear adalah suatu tren yang tidak membentuk garis lurus. Ada dua jenis:
- Model Kuadratik
- Model Ekponensial
Model Tren Linear merupakan model peramalan suatu variabel dengan menggunakan variabel bebasnya waktu. rumus untuk menghitung Forecasting :
Y = a + bx
Dimana :
Y = nilai tren atau variabel yang akan diramalkan
a = bilangan konstant
b = slope atau koefisien garis trend
x = indeks waktu (dimulai dari 0,1,2.........n)
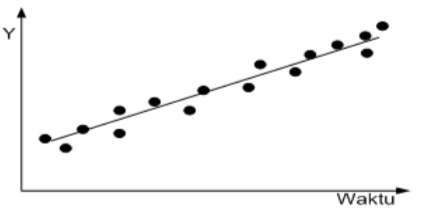
Tren dapat berupa tren naik yang disebut tren positif dan dapat pula berupa tren turun yang disebut tren negatif. Disebut tren positif apabila variabel yang diteliti (Y) menunjukkan gejala kenaikan atau menunujukkan rata-rata pertambahan. Tren negatif apabila variabel yang diteliti (Y) menunujukkan gejala semakin menurun atau menunujukkan rata-rata penurunan.
Metode Least Square (kuadrat kecil) adalah metode yang digunakan untuk menentukan persamaan trend data yang mencakup analisis Time Series dengan dua kasus data genap dan ganjil. Kuadrat terkecil (least square) merupakan metode yang paling banyak dipakai untuk menentukan persamaan trend data, karena menghasilkan "line of best fit". Garis trend ini mempunyai sifat penjumlahan seluruh diviasi vertikal titik-titik data terhadap garis adalah nol. Penjumlahan seluruh kuadrat deviasi vertikal data historis dari garis adalah minimum. Garis melalui rata-rata X dan Y. Untuk persamaan linear, garis trend dicari dengan penyelesaian simultan nial a dan b pada dua persamaan normal berikut :
Σ Y = n a + b Σ X
Σ XY = a Σ X + b Σ X^ (kuadrat)
Bila titik tengah data sebagai tahun dasar, maka Σ X = 0 dan dapat dihilangkan dari persamaan diatas, sehingga menjadi :
Σ Y = n a → a = Σ Y / n
Σ XY = b Σ X^ (kuadrat) ⟶ b = Σ XY / Σ X^ (kuadrat)
Bila ada sejumlah periode ganjil, titik tengah periode waktu detentukan X=0, sehingga julah plus dan minus sama dengan nol (0). Seperti tabel dibah ini.
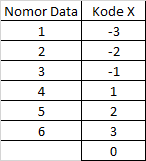
Tetapi jika jumlah data adalah genap, prosedur pemberian kode seperti tabel di bawah ini :
- Praktik perhitungan Least Square
Keterangan :
a = Σ Y / n = 1424/16 = 89
b = Σ XY / Σ X^ = 446/408 = 1,1
Jadi, persamaan peramalan dalam bentuk Y = a +bX adalah :
Y = 89 + 1,1 X
Forecasting untuk kuartal pertama tahun 1985 adalah sebesar 98,9 unit dengan perhitungan :
Y = 89 + 1,1 (9) = 98,9
Metode unutk mencari garis trend dengan perhitungan statistika dan metematika tertentu guna mengetahui fungsi garis lurus sebagai pengganti garis patah - patah yang dibentuk oleh data historis. Bila periode pertama sebagai tahun dasar X=0. Apabila pertimbangan data ganjil dan data genap ingin diabaikan, tanpa khawatir terjadi kesalahan dalam melakukan perhitungan peramalan, maka cara berikut ini dapat menjadi pilihan. Untuk mendapatkan nilai a dan b, rumus yang digunakan adalah :
a = (ΣY ΣX^ - ΣX ΣXY) / (n. ΣX^ - (ΣX)^)
b = (n. ΣXY - ΣX ΣY) / (n. ΣX^ - (ΣX)^)
Apabila cara ini yang dipilih, maka untuk mendapatkan nilai a dan b, rumus yang digunakan adalah :
a = (ΣY ΣX^ - ΣX ΣXY) / (n. ΣX^ - (ΣX)^)
a = (222(30) - 10(441)) / (5(30) - (10)^2)
= 45
b = (n. ΣXY - ΣX ΣY) / (n. ΣX^ -(ΣX)^)
b = (5(441) - 10(222)) / (5(30) - (10)T^2)
= -0,3
Y = a + bX
Y = 45 - 0,3X > 45 - 0,3(5) > 45 - 1,5 > 43,5
Trend kuadratik merupakan trend yang nilai variabel tak bebaskan naik atau turun secara linier atau terjadi parabola bila datanya dibuat plot (hubungan variabel dependen dan independen). Persamaan Trend Kuadratik :
Y = a + bX + cX^
Keterangan :
Y = nilai trend yang diproyeksikan
a,b,c = konstanta (nilai koefisien)
X = waktu (tahun)
Rumus 1 :
Dengan menggunakan rumus tiga persamaan normal :
ΣY = n. a + b ΣX + c ΣX^2
ΣXY = a ΣX + b ΣX^2 + c ΣX^3
ΣX^2Y = a ΣX^2 + b ΣX^3 + c ΣX^4
a = ((ΣY ΣX^4) - (ΣX^2Y ΣX^2)) / (n ΣX^4 - (ΣX^2)^2)
b = ΣXY / ΣX^2
c = n (ΣX^2Y) - (ΣX^2) (ΣY) / n (ΣX^4) - (ΣX^2)^2
Adalah suatu trend yang mempunyai pangkat atau eksponen dari waktunya. Bentuk persamaan eksponensial dirumuskan sebagai berikut :
Y' = a (1+b) pangkat X → In
Y' = a.b pangkat X → log
Rumus 1 --> LOG :
log Y' = log a + x log b
log a = Σ log Y / n
log b = Σ (x. log Y) / Σ X^2
Rumus 2 --> LN :
Y' = a (1 + b) pangkat X
LN Y' = Ln a + X Ln (1+b)
sehingga a = anti In (Σ LnY)/n
b= anti In Σ (X. LnY)-1 / ΣY^2
>>>>> Semoga Bermanfaat <<<<<





Komentar
Posting Komentar